激光喷丸参数对 7075 铝合金残余应力分布影响规律的数值分析

飞机服役一定年限后, 其结构件存在大量的腐 蚀损伤, 时刻威胁着飞机的飞行安全 。 因此, 解 决材料表面腐蚀损伤问题、 提高金属材料耐应力腐 蚀性能显得尤为迫切。 目前, 国内外通常采用表面 强化技术来改善材料的耐应力腐蚀性能。 与其他 表面强化技术相比, 激光喷丸具有灵活可控、 应变 率高、 效果显著等特点, 因而在航空航天领域具有 较为广阔的应用前景 。 掌握各种不同激光喷丸工艺参数对材料表面残余应力分布的影响规律, 将有 助于更加快捷地获取所期望的残余应力分布, 为实 际飞机维修工作提供一定的理论指导。

在激光喷丸参数对残余应力分布影响规律方面, 周建忠 、 胡永祥 等分别以 2024 – T3 铝合金和 35CD4 50HRC 钢为研究对象, 通过有限元模拟发 现, 材料表面残余压应力随着冲击次数的增加而增 加, 压应力影响层深度也随之增加。 陈瑞芳等[6] 借 助 ANSYS 软件对激光喷丸 40Cr 钢试样分析发现,材料表面残余压应力随冲击波峰值压力的增加而增 加, 当峰值压力增加至一定值时, 材料表面残余压 应力达到最大并不再增加。 黄舒等[7] 利用 ABAQUS软件对 6061 – T6 铝合金试样模拟分析发现, 试样残余应力场随光斑尺寸的增加而增加。 钱绍祥等通过激光冲击 AISI202 不锈钢焊接接头试验发现, 提高光斑搭接率可以优化激光喷丸后焊接接头的应 力分布, 提高材料表面压应力水平。 掌握不同激光 喷丸参数对材料表面残余应力分布的影响规律有助 于激光喷丸在实际操作过程中更好地运用。

本文以飞机常用 7075 航空铝合金靶材为研究对 象, 利用有限元软件 ABAQUS 对激光喷丸过程进行 数值模拟, 分析 7075 铝合金靶材在不同峰值压力、 冲击次数、 光斑大小及搭接率等条件下材料表面残 余应力分布情况, 获取各不同工艺参数对材料表面 及内部残余应力分布的影响规律, 为实际的飞机维 修工作奠定一定的理论基础。

1  冲击波压力模型

由于激光喷丸过程中, 冲击波对材料的作用过程极为复杂, 因而难以运用有限元软件 ABAQUS 对 其进行精确的数值模拟。 目前, 国内外学者一般选 择将冲击波对材料作用等效为随时间变化的压力对 材料的作用。 1990 年, Fabbro R 等通过对毫米尺度 约束模型下冲击波的半理论研究, 提出冲击波峰值 压力与激光功率密度的关系如下 :

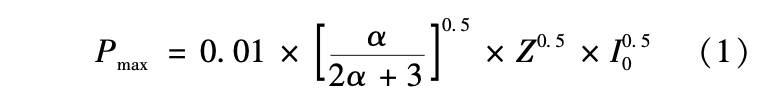
式中: Pmax 为峰值压力; α 为等离子体的比热比; Z 为固体靶及约束层对冲击波的声阻抗; I0 为激光功 率密度。

Zhang W W 等沿用 Fabbro R 等的理论, 但其认 为激光能量随其与光斑中心距离呈准高斯分布趋势, 并得到冲击波峰值压力随空间分布关系如下 :

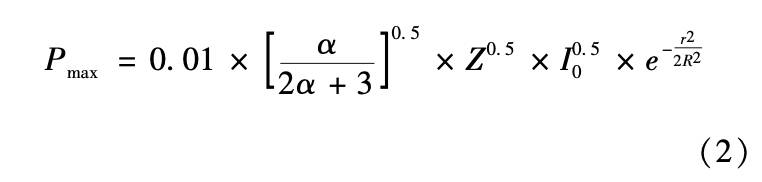
式中: r 为某点与光斑中心距离; R 为光斑半径。 本文采用式 (2) 对冲击波峰值压力随空间分 布关系进行计算, 采用的激光器基本参数为光斑能 量2J,脉宽≤10ns,焦点直径Ф2mm,通过计算 可得, 光斑中心处冲击波峰值压力最大可达到3. 4 GPa。

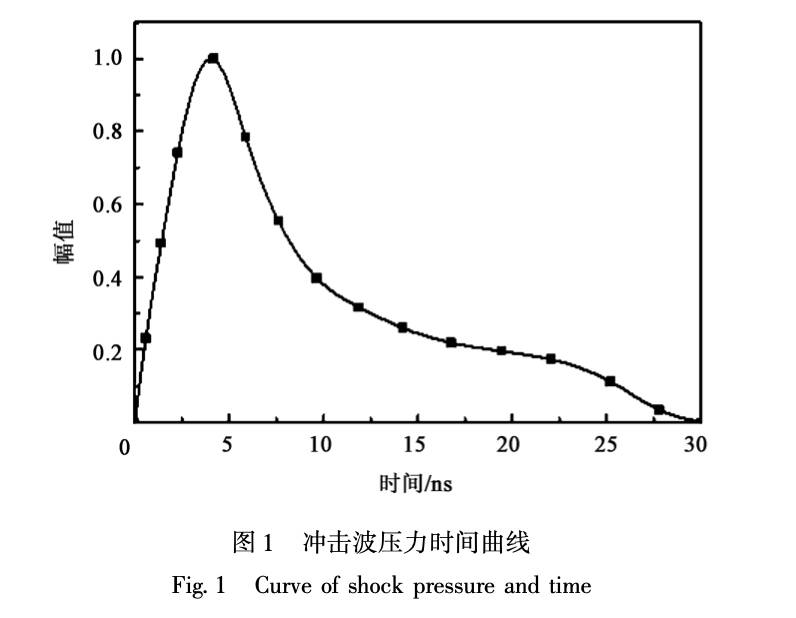
Peyre P 等通过试验研究发现, 冲击波压力作用时间为激光脉宽的 3 ~ 4 倍。 本文所采用激光 器脉宽为 10 ns, 故而冲击波压力作用时间可取30ns模拟采用的冲击波压力随时间变化曲线如图1所示。

2  材料的本构模型

激光喷丸是利用短脉冲 (几十 ns)、 高峰值功 率密度 ( > 109 W·cm – 2 ) 的激光束辐射金属材料 表面, 其应变速率极高 ( >10的6次方 /S)。 激光喷丸过 程中, 由于金属材料表面吸收层的隔热作用, 金属 材料的塑性变形可看做冷变形, 材料表面只受到冲 压力的作用。 材料屈服强度和流体应力随着应变率 的提高而提高, 而硬化率则会随之降低, 因此, 可 近似采用理想弹塑性材料模型。 在一维应变条件下, 材料的初始屈服极限应力可定义为 Hugoniot 弹性极 限 (σHEL)。 当材料中应力波压力小于 σHEL 时, 材 料处于弹性极限范围内, 只会发生弹性变形; 当压 力大于 σHEL 时, 材料将产生无法恢复的塑性变形; 当材料中应力波压力达到 σHEL 时, 材料产生屈服。 材料的动态屈服强度 σr 计算式如下 :

式中: v 为材料的泊松比。 7075 航空铝合金机械性能如表 1 所示 。

3  有限元模型的建立

激光冲击处理 7075 铝合金靶材, 由于激光光斑为圆形, 其在材料表面的压力作用区域亦为圆形, 且冲击波压力成中心对称, 为提高计算机运算速率, 仅对模型1/2进行建模。 本文在建模时, 将模型简 化为20 ×8 ×4 的立方体, 如图2 所示, 其中1/2 圆 形为冲击波压力作用范围。 胡永祥[13] 通过研究发 现, 激光喷丸冲击波主要沿纵向传播, 因而对纵向 网格尺寸要求远远高于横向网格。 在横向上, 对激 光喷丸区域, 采用R/Lxy =20 (Lxy为激光喷丸模型 横向尺寸大小) 进行网格划分。 纵向上, 越靠近激 光冲击区域表面需要越细的网格, 而对靠近下表面 的网格尺寸要求较低。 因此, 本文采用 single 的布 种方法, 从模型上表面到下表面, 其种子分布间 距呈等比数列递增。 为提高运算效率, 对模型非 关键部分选用较为粗大的网格进行划分。 得到的 激光喷丸有限元模型如图 2 所示, 其单元类型为 C3D8R, 单元数量为 137025, 模型的剖面设置为 对称边界。

4  模拟结果及分析

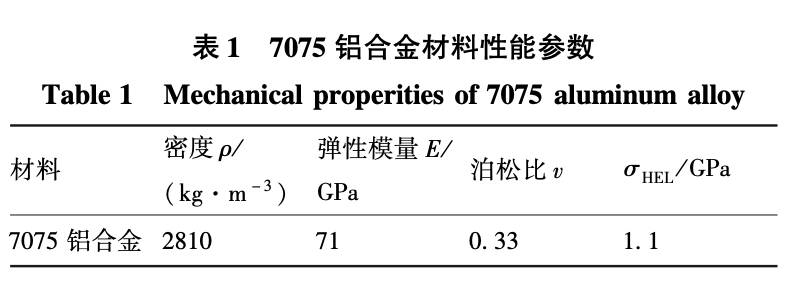
利用有限元软件 ABAQUS 对激光喷丸过程进行 数值模拟, 当冲击波峰值压力为 2. 04 GPa、 光斑直 径为 Ф4 mm、 脉宽为 10 ns 时, 最终得到的稳定残 余应力场如图 3 所示。

图 4 为激光喷丸后 7075 铝合金沿表面方向及深度方向的残余应力分布曲线。 由图 3 及图 4a 可知,当冲击波峰值压力为 2. 04 GPa 时, 材料表面残余应力最大值出现在光斑中心处, 即图 4a 中的 A 点处,为 – 315. 9 MPa。 随着距光斑中心距离的增加, 材料表面残余压应力逐渐减小, 其原因主要是光斑中心处激光功率密度较高, 产生冲击波峰值压力较大, 而边缘处激光功率密度较低, 产生的冲击波压力也较小, 造成光斑中心残余压应力较大

而边缘处残余应力较小。 在距光斑中心 1 mm 处, 即图 4a 中 B 点处, 材料表面残余压应力减小为 -237.7MPa。 在光斑边缘处, 如图4a中C点所 示, 材料表面残余压应力进一步减小为 – 30. 9 MPa。 由图 4b 可知, 材料内部残余压应力随着深 度的加深而逐渐减小,约在0.37mm处(图4b中 D 点) 减小为 0, 即残余压应力影响层深度为 0. 37mm。 当深度进一步加深时材料内部出现残余拉应力并逐渐较小为 0。

5  激光喷丸参数对残余应力分布的 影响规律

5. 1  冲击波峰值压力对残余应力分布的影响规律 冲击波峰值压力大小是影响残余应力分布的一 个关键性因素。 由激光器基本参数并根据式 (2) 计算可知, 激光器所能提供的最大冲击波峰值压力 为 3. 4 GPa, 在模拟时选取冲击波峰值压力应小于

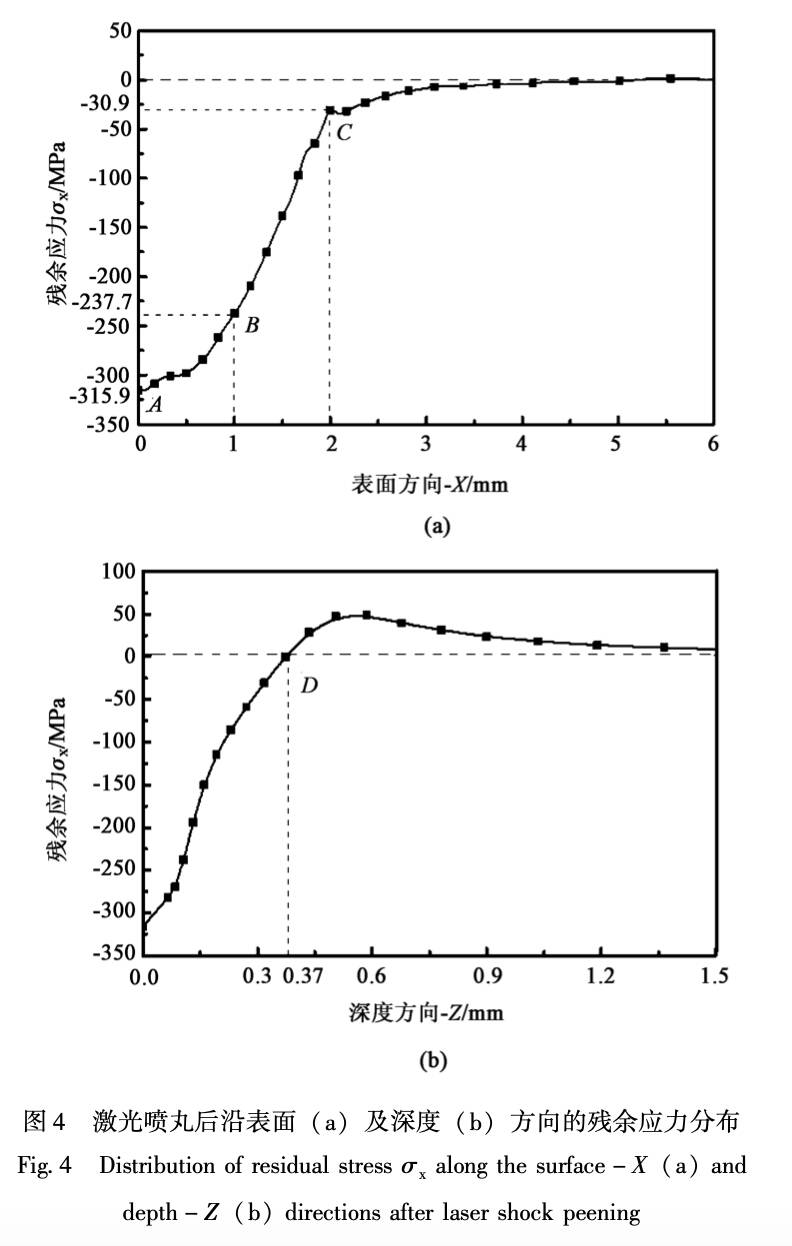
该值。 选取冲击波峰值压力 P 分别为 0. 5Pmax, 0. 6Pmax, 0. 7Pmax, 0. 8Pmax, 0. 9Pmax, 即 1. 7, 2. 04, 2. 38, 2. 72 和3. 06 GPa 进行有限元模拟, 其 他激光喷丸参数为: 冲击波压力作用时间 30 ns、 光 斑大小 Ф4 mm、 冲击 1 次, 得到不同峰值压力下残余应力 σx 沿表面方向及深度方向分布曲线, 如图 5所示, 由图 5 可以给出以下结果。

(1) 冲击波峰值压力的大小对材料表面及内部 残余应力分布有较大的影响。 当峰值压力为1. 7 GPa时, 材料表面残余压应力最大值为 – 196. 3 MPa, 位于光斑中心处; 材料表面最大残余压应力随冲击波 峰值压力的增加而增加。 当冲击波峰值压力为 2. 72 GPa 时, 材料表面峰值压力达到最大。 进一步 增加峰值压力时, 材料表面残余压应力几乎不再增 加。 其原因主要是冲击区域材料塑性变形趋于饱和, 使残余压应力难以提高。

(2) 材料内部最大残余压应力及残余压应力影 响层深度随着冲击波峰值压力的增加而增加, 当峰 值压力为 1. 7 GPa 时, 残余压应力影响层深度为 0. 37 mm。 当峰值压力增加至 3. 06 GPa, 残余应力 影响层深度增加至 0. 49 mm。

(3) 当峰值压力为2. 72 和3. 06 GPa 时, 靶材 表面均出现了明显的残余应力洞现象, 即残余压 应力峰值并不出现在冲击区域的几何中心, 而是 出现在距中心一定距离的环形区域。 且随着冲击 波峰值压力的增加, 残余应力洞现象越明显。 这 主要是由于冲击波峰值压力越大, 冲击区域边缘 边界效应产生的诸如 Rayleigh 波和切应变波等强度越 大, 造成冲击区域中心材料反向塑性变形越显著[14]。

5. 2  冲击次数对残余应力分布的影响规律 

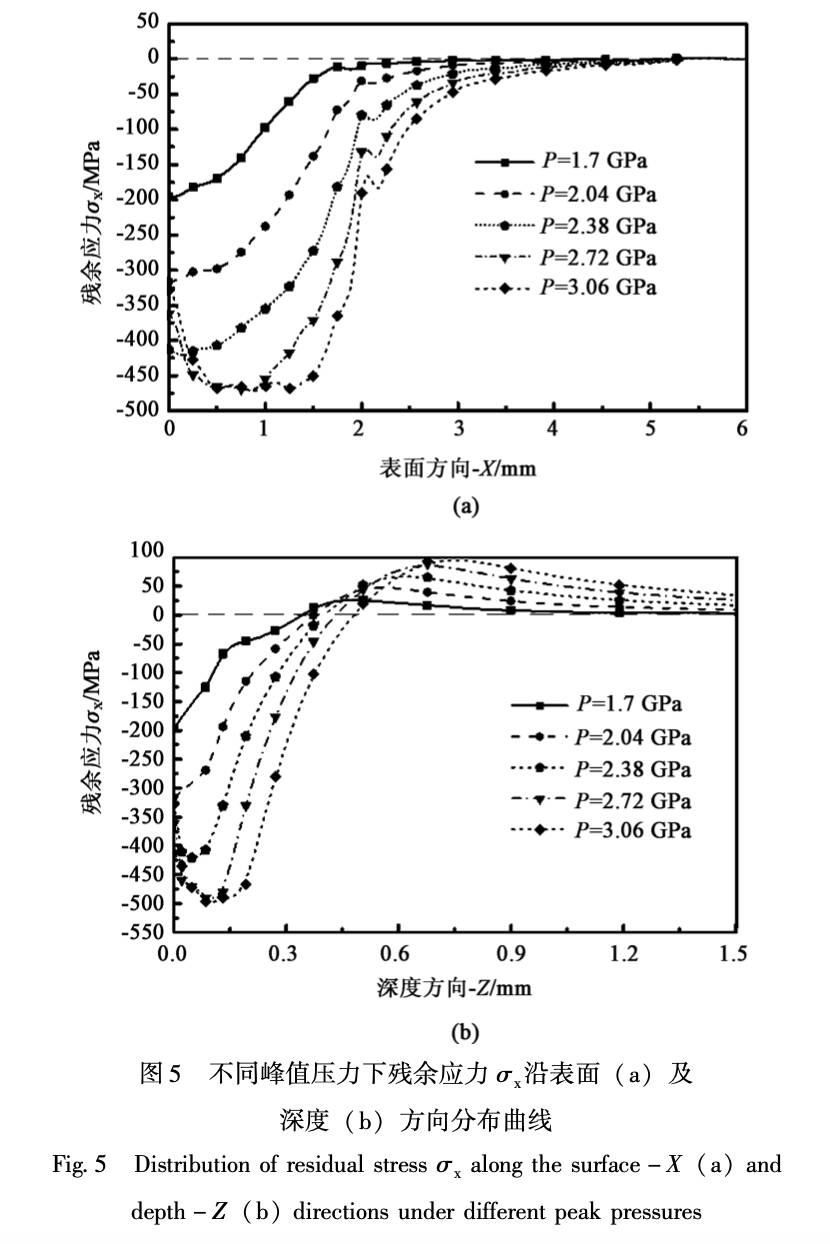
在某些情况下, 为了使靶材表面及内部达到较 大的残余压应力值, 但由于设备功率限制, 无法在 一次冲击后实现时, 可采用单点多次冲击[5] 。 为了研究激光冲击次数 T 对残余应力分布的影响规律, 分别对靶材进行单点 1 ~ 5 次冲击进行数值分析, 其 他激光喷丸参数为峰值压力 2. 2 GPa、 光斑直径 Ф4 mm、 冲击波压力持续时间 30 ns。 得到不同冲击 次数下残余应力 σx 沿表面方向及深度方向的分布曲 线, 如图 6 所示, 可以得出以下结果。

(1) 随着冲击次数的增加, 材料表面残余压应 力增加。 当冲击次数T由1增加至5时, 材料表面 最大残余压应力值分别为 – 369.3, – 404.2,-424.5, -443.1和-454.7MPa,冲击2,3,4 和 5 次后残余压应力最大值分别相对前一次冲击后 残余压应力最大值增加 9. 45% , 5. 02% , 4. 38% 和2. 61% 。 由此可见, 在冲击第 2 次时, 材料表面最 大残余应力增长幅度最大, 为9.45%, 再增加冲击 次数时, 其增益效果减弱。 其原因是由于多次冲击 后, 材料产生硬化现象, 再次产生塑性变形必须在 材料表面施加更大的冲击压力。

(2) 材料内部最大残余压应力及残余压应力影 响层深度随着冲击次数的增加而增加。 当冲击次数 从 1 增加至 5 时, 残余压应力影响层深度分别为 0.39, 0.47, 0.52, 0.56 和 0.58 mm。 由此可见,随着冲击次数的增加, 残余压应力影响层深度增益 效果减弱。

5. 3 光斑大小对残余应力分布的影响规律

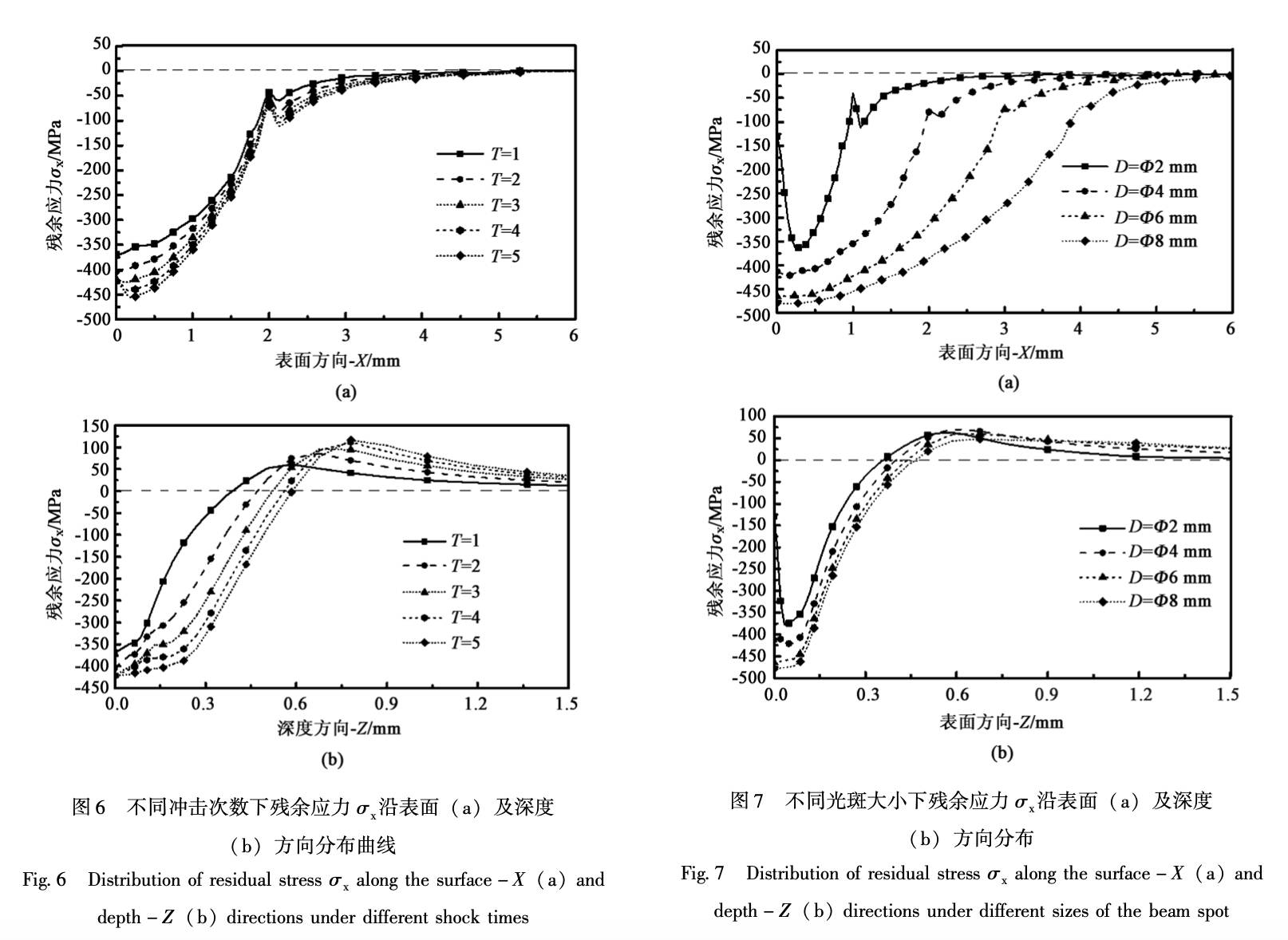
为了探索光斑大小对激光喷丸残余应力分布的 影响规律, 选取直径 D 分别为 Ф2, Ф4, Ф6 和 Ф8 mm 的光斑进行数值分析。 其他激光喷丸工艺参 数为: 峰值压力 2. 38 GPa、 冲击波压力持续时间 30 ns、 冲击 1 次, 得到的不同光斑大小下残余应力 σx沿表面方向及深度方向的分布曲线, 如图7所示, 由图 7 可以得出以下结果。

(1) 当光斑直径分别为 Ф2, Ф4, Ф6 和 Ф8 mm 时, 材料表面最大残余应力分别为 – 363.2, -421.2, – 464.9 和 – 479.3 MPa。 光斑直径为Ф4, Ф6, 和 Ф8 mm 分别相对光斑半径为 R2 mm 时表面最大残余压应力增加 15.9%, 28.0% 和31. 97% 。 由此可知, 材料表面残余压应力随着光斑尺寸的增加而增加。 当光斑尺寸增大到一定值时,其表面最大残余压应力增益效果减弱。 其原因主要是小直径光斑下冲击波在材料内部传播类似球面波,大光斑直径下冲击波在材料内部传播类似平面波,球面波的衰减速率远大于平面波。

2) 当光斑尺寸分别为 Φ2, Φ4, Φ6 和Φ8 mm 时, 残余压应力影响层深度分别为 0. 36, 0. 40, 0. 43, 和 0. 46 mm。 由此可见, 在峰值压力一定时,残余应力影响层深度随着光斑尺寸的增加而增加。

(3) 当光斑直径为 Φ2 mm 时, 靶材表面出现 了非常明显的残余应力洞现象, 且残余应力洞现象 随着光斑尺寸的增大而逐渐消失。 这主要是由于光 斑直径越大, 光斑边界效应越小, 产生的稀疏波的 强度越低, 且大光斑下稀疏波传播行程长, 汇聚到 光斑中心时强度进一步减弱, 造成冲击区域中心反 向塑性变形较小。

5. 4  光斑搭接率对残余应力分布的影响规律 

在激光喷丸过程中, 为了使靶材表面冲击波峰 值压力达到某一大小, 激光器需保证一定的功率密 度。 由于激光器本身功率限制, 在激光喷丸时选用 的光斑不宜过大, 单个光斑不可能对整个待冲击区 域一次性冲击强化处理。 因而, 在实际激光喷丸过 程中需采用一定的光斑搭接处理工艺。 光斑搭接率计算公式为[8] :

p = (1 – L / D) × 100% (4)

式中: L 为两相邻光斑间距离; D 为光斑直径。

为研究光斑搭接率对残余应力分布的影响规律, 分别采用搭接率为 0% , 25% , 50% 和 75% 进行模 拟, 激光喷丸参数选择冲击波峰值压力 2. 04 GPa、 光斑直径 Ф 4 mm、 冲击波压力作用时间 30 ns、 冲击 1 次, 得到的不同搭接率时材料表面残余应力 σx 沿表面 X 方向分布规律, 如图 8 所示, 图中圆形区 域为激光冲击区域。 图 9 为不同搭接率下残余应力 σx 沿材料表面 X 方向分布曲线对比。

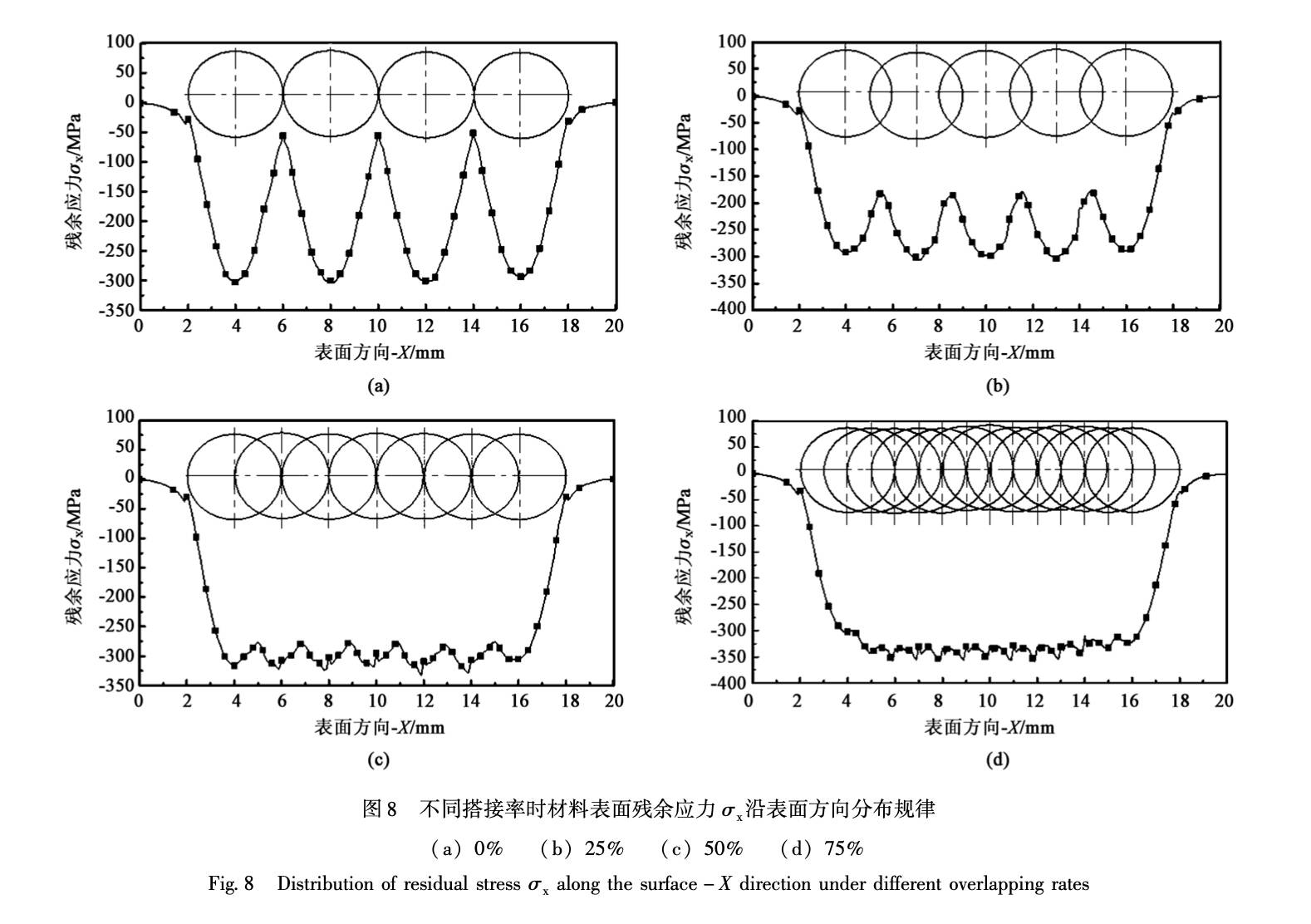
由图8a可知, 当光斑搭接率为0%时, 由于相邻光斑之间不存在任何搭接, 因而各次激光喷丸过程是相对独立的过程, 材料表面残余压应力极大值出现在光斑中心处, 极小值出现在各激光冲击区域边缘处, 且材料表面残余压应力波动较明显。 由图8b可知, 当光斑搭接率为25%时, 由于相邻光斑之 间存在少量搭接, 且各激光冲击区域中心不存在搭 接, 因而材料表面残余压应力极大值出现在激光冲 击区域中心处。 而在冲击边缘处, 由于与后一冲击 区域光斑半径中点搭接, 使该处残余压应力得到较 大改善, 残余压应力极小值并未出现在光斑边缘处, 而是出现在相邻两光斑搭接区域中点处。 且材料表 面残余压应力波动值较搭接率为 0% 时减小很多。 由图 8c 可知, 当搭接率为 50% 时, 前一冲击区域 中心正好与下一冲击区域边缘搭接, 前一冲击区 域边缘恰好与后一冲击区域中心搭接, 由于冲击 区域中心残余压应力较大, 冲击区域边缘压应力 较小, 搭接后材料表面残余应力波动值较搭接率 为25%时有明显改善。 残余压应力极大值出现在 冲击区域中心, 极小值出现在光斑半径中点处。 由图8d可知, 当光斑搭接率为75%时, 前1 个冲 击区域中心正好与后 1 个冲击区域半径中点处及 其后第 2 个冲击区域边缘处搭接, 由于冲击区域中心残余应力值较大, 搭接后材料表面残余应力极 大值出现在该区域。 材料表面残余应力波动值在搭 接率为 75% 时更小。

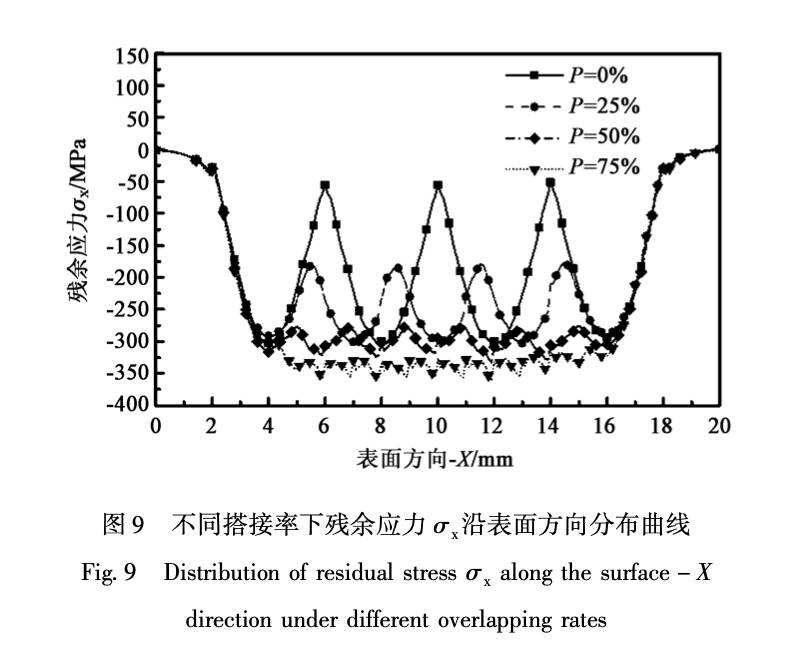
由图 9 可知, 材料表面整体残余压应力随着光 斑搭接率的增加而增加。 其原因主要是光斑搭接率 越大, 同一区域激光冲击次数越多, 因而其残余压 应力越大。

6  结论

(1) 材料表面残余压应力随冲击波峰值压力的 增加而增加。 当峰值压力增加至一定值 (如7075 航 空铝合金靶材当光斑半径为 R4 mm 时、 峰值压力为 2. 72 GPa) 时, 材料表面残余压应力达到最大。 过 大的冲击波峰值压力作用在材料表面会在冲击区域 中心处产生极为明显的残余应力洞现象, 在实际激 光喷丸过程中应尽量避免。

(2) 随着冲击次数的增加, 材料表面残余压应 力增加。 但当冲击次数达到一定值 (本文中对应冲 击次数为 3 次) 时, 其增益效果减弱。 在实际激光 喷丸过程中, 为提高生产效率, 应尽量避免采用过 多的冲击次数。

(3) 光斑搭接率是影响材料表面残余应力分布 的一个重要参数。 当搭接率为 75% 时, 材料表面残 余应力较大, 且沿表面方向波动较小, 在实际操作 中应优先选取。

江苏激光喷丸设备制造商，激光喷丸代工服务商，竭诚为您服务